COMPOSING PROGRAMS¶

约 2713 个字 651 行代码 2 张图片预计阅读时间 22 分钟共被读过次

1 使用函数构建抽象 ¶

1.1 开始 ¶

程序由两部分组成 :

计算一些值
执行一些操作
函数
对象
解释器 :
- 用于计算复杂表达式的程序
增量测试、模块化设计、明确的假设和团队合作

1.2 编程要素 ¶

1.2.1 表达式 ¶

语言要有的机制 :
- 原始表达式和语句：语言所关心的最简单的个体
- 组合方法：由简单元素组合构建复合元素
- 抽象方法：命名复合元素，并将其作为单元进行操作
infix notation

1.2.2 调用表达式 ¶

subexpressions
用参数来调用函数
nested（嵌套）

1.2.3 导入库函数 ¶

1.2.4 名称与环境 ¶

= is assignment operator
- 最简单的抽象方法
environment

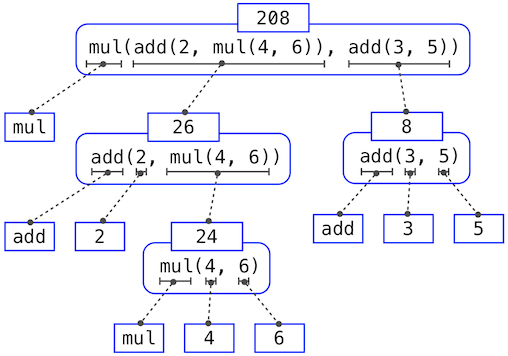
1.2.5 求解嵌套表达式 ¶

求值程序本质上是递归的

表达式树

1.2.6 非纯函数 print ¶

Pure functions
None-pure functions
which has a side effect

1.3 定义新的函数 ¶

Python

def <name>(<formal parameters>):
    return <return expression>

1.3.1 环境 ¶

environment has some frames
frames have some bindings

intrinsic name
bound name
不同的名称可能指的是同一个函数，但该函数本身只有一个内在名称
对函数形式参数的描述被称为函数的签名

1.3.2 调用用户定义的函数 ¶

在新的局部帧中，将实参绑定到函数的形参上。
在以此帧开始的环境中执行函数体。
name evaluation

1.3.3 示例：调用用户定义的函数 ¶

1.3.4 局部名称 ¶

1.3.5 选择名称 ¶

PEP 8 – Style Guide for Python Code | peps.python.org

1.3.6 抽象函数 ¶

functional abstraction
- domain
- range
- intent

1.3.7 运算符 ¶

truediv
floordiv

1.4 设计函数 ¶

一个函数一个任务
Don't repeat yourself (DRY)
定义通用的函数

1.4.1 文档 ¶

docstring

1.4.2 参数默认值 ¶

1.5 控制 ¶

1.5.1 语句 ¶

assignment
def
return

1.5.2 复合语句 ¶

header
suite

Python

<header>:
    <statement>
    <statement>
    ...
<separating header>:
    <statement>
    <statement>
    ...
...

def 是复合语句
the header controls its suite
这个定义揭示了递归定义序列（sequence）的基本结构：一个序列可以分解成它的第一个元素和其余元素
redirected control

1.5.3 定义函数 II：局部赋值 ¶

1.5.4 条件语句 ¶

Python

if <expression>:
    <suite>
elif <expression>:
    <suite>
else:
    <suite>

1.5.5 迭代 ¶

iteractive control

Python

while <expression>:
    <suite>

1.5.6 测试 ¶

assertions

Python

>>> assert fib(8) == 13, '第八个斐波那契数应该是 13'

Doctests

Python

>>> def sum_naturals(n):
    """返回前 n 个自然数的和。

    >>> sum_naturals(10)
    55
    >>> sum_naturals(100)
    5050
    """
    total, k = 0, 1
    while k <= n:
        total, k = total + k, k + 1
    return total

Python

>>> from doctest import testmod
>>> testmod()
TestResults(failed=0, attempted=2)

单个函数的交互

Python

>>> from doctest import run_docstring_examples
>>> run_docstring_examples(sum_naturals, globals(), True)
Finding tests in NoName
Trying:
    sum_naturals(10)
Expecting:
    55
ok
Trying:
    sum_naturals(100)
Expecting:
    5050
ok

1.6 高阶函数 ¶

general patterns
named concepts
higher-order functions
- 可以把函数当作参数或者返回值

1.6.1 作为参数的函数 ¶

slots
step through （单步调试）
一个几乎没必要看的例子 :

Python

>>> def summation(n, term):
        total, k = 0, 1
        while k <= n:
            total, k = total + term(k), k + 1
        return total
>>> def identity(x):
        return x
>>> def sum_naturals(n):
        return summation(n, identity)
>>> sum_naturals(10)
55

1.6.2 作为通用方法的函数 ¶

user-defined functions
general methods
iterative improvement
repetitive refinement

1.6.3 定义函数 III：嵌套定义 ¶

两个后果 :

全局帧变混乱
函数签名限制
Nested function definition
Lexical scope
- 这种在嵌套定义之间共享名称的规则称为词法作用域

每个用户定义的函数都有一个父环境：定义它的环境。
调用用户定义的函数时，其局部帧会继承其父环境。

关键优势 :
- 局部函数的名称不会影响定义它的函数的外部名称，因为局部函数的名称将绑定在定义它的当前局部环境中，而不是全局环境中。
- 局部函数可以访问外层函数的环境，这是因为局部函数的函数体的求值环境会继承定义它的求值环境。
Extended Environments
局部定义的函数通常被称为闭包（closures）

1.6.4 作为返回值的函数 ¶

composition

1.6.5 示例：牛顿法 ¶

1.6.6 Currying¶

uncurrying transformation

Python

>>> def curry2(f):
        """返回给定的双参数函数的柯里化版本"""
        def g(x):
            def h(y):
                return f(x, y)
            return h
        return g
>>> def uncurry2(g):
        """返回给定的柯里化函数的双参数版本"""
        def f(x, y):
            return g(x)(y)
        return f
>>> pow_curried = curry2(pow)
>>> pow_curried(2)(5)
32
>>> map_to_range(0, 10, pow_curried(2))
1
2
4
8
16
32
64
128
256
512

1.6.7 Lambda 表达式 ¶

Python

lambda              x         :              f(g(x))
"A function that    takes x   and returns    f(g(x))"

\(\displaystyle \lambda\)

Python

>>> s = lambda x: x * x
>>> s
<function <lambda> at 0xf3f490>
>>> s(12)
144

1.6.8 抽象和一等函数 ¶

first-class status

可以与名称绑定
可以作为参数传递给函数
可以作为函数的结果返回
可以包含在数据结构中

1.6.9 函数装饰器 ¶

decorator

Python

>>> def trace(fn):
        def wrapped(x):
            print('-> ', fn, '(', x, ')')
            return fn(x)
        return wrapped

>>> @trace
    def triple(x):
        return 3 * x

>>> triple(12)
->  <function triple at 0x102a39848> ( 12 )
36

annotation
等价于 :

Python

>>> def triple(x):
        return 3 * x
>>> triple = trace(triple)

1.7 递归函数 ¶

rucursive
circular nature

1.7.1 递归函数剖析 ¶

base case
unwinds
recursive calls
induction

1.7.2 mutually recursive¶

1.7.3 递归函数中的打印 ¶

abstraction barrier

1.7.4 tree recursive¶

1.7.5 示例：分割数  ¶

Python

>>> def count_partitions(n, m):
        """计算使用最大数 m 的整数分割 n 的方式的数量"""
        if n == 0:
            return 1
        elif n < 0:
            return 0
        elif m == 0:
            return 0
        else:
            return count_partitions(n-m, m) + count_partitions(n, m-1)

>>> count_partitions(6, 4)
9
>>> count_partitions(5, 5)
7
>>> count_partitions(10, 10)
42
>>> count_partitions(15, 15)
176
>>> count_partitions(20, 20)
627

2 使用数据构建抽象 ¶

2.1 引言 ¶

高阶函数使我们能够根据通用的计算方法进行操作和推理，从而增强了语言的功能。这就是编程的本质
有效使用内置数据类型和用户定义的数据类型是数据处理型应用（data processing applications）的基础

2.1.1 原始数据类型 ¶

原始数据类型具有属性 :

有一些可以求解为原始数据类型的表达式，被称为字面量（literals）。
有用于操作原始类型值的内置函数和操作符。 - 原始数字类型
- int
- float
- complex
- Non-numeric types
- bool
- more on 原始数据类型

2.2 数据抽象 ¶

2.2.1 示例：有理数 ¶

wishful thinking

Python

>>> def add_rationals(x, y):
        nx, dx = numer(x), denom(x)
        ny, dy = numer(y), denom(y)
        return rational(nx * dy + ny * dx, dx * dy)

>>> def mul_rationals(x, y):
        return rational(numer(x) * numer(y), denom(x) * denom(y))

>>> def print_rational(x):
        print(numer(x), '/', denom(x))

>>> def rationals_are_equal(x, y):
        return numer(x) * denom(y) == numer(y) * denom(x)

2.2.2 pair¶

from operator import getitem

Python

>>> def rational(n, d):
        return [n, d]

>>> def numer(x):
        return x[0]

>>> def denom(x):
        return x[1]

简化有理数 :

Python

>>> from fractions import gcd
>>> def rational(n, d):
        g = gcd(n, d)
        return (n//g, d//g)

2.2.3 抽象屏障 ¶

数据抽象 : 用一组基本操作来操作数据。
avbstraction barrier
the best:

Python

>>> def square_rational(x):
    return mul_rational(x, x)

2.2.4 数据的属性 ¶

相当于自己写一个数据结构 :

Python

>>> def pair(x, y):
        """Return a function that represents a pair."""
        def get(index):
            if index == 0:
                return x
            elif index == 1:
                return y
        return get

>>> def select(p, i):
        """Return the element at index i of pair p."""
        return p(i)

>>> p = pair(20, 14)
>>> select(p, 0)
20
>>> select(p, 1)
14

2.3 序列 ¶

sequence
- Length
- Element selection

2.3.1 list¶

2.3.2 序列遍历 ¶

Python

for <name> in <expression>:
    <suite>

the expression must produce an iterable object
sequence unpacking

Python

>>> pairs = [[1, 2], [2, 2], [2, 3], [4, 4]]
>>> same_count = 0
>>> for x, y in pairs:
        if x == y:
            same_count = same_count + 1
>>> same_count
2

range

2.3.3 序列处理 ¶

list comprehensions

Python

>>> odds = [1, 3, 5, 7, 9]
>>> [x+1 for x in odds]
[2, 4, 6, 8, 10]
[<map expression> for <name> in <sequence expression> if <filter expression>]

Aggregation 就是缩并啦
- sum
- min
- max

Python

>>> def apply_to_all(map_fn, s):
    return [map_fn(x) for x in s]
>>> def keep_if(filter_fn, s):
    return [x for x in s if filter_fn(x)]
# conventional names
>>> apply_to_all = lambda map_fn, s: list(map(map_fn, s))
>>> keep_if = lambda filter_fn, s: list(filter(filter_fn, s))

2.3.4 序列抽象 ¶

Membership
- in
- not in
Slicing

2.3.5 字符串 ¶

string
没有字符类型

Membership
Multiline Literals
String Coercion
more on Dive Into Python 3 的字符串章节提供了字符编码和 Unicode 的描述

2.3.6 树 ¶

closure property
bax-and-pointer notation

root label
branch
leaf: the tree without branch
node
tree-recursive
两个例子:

Python

>>> def fib_tree(n):
        if n == 0 or n == 1:
            return tree(n)
        else:
            left, right = fib_tree(n-2), fib_tree(n-1)
            fib_n = label(left) + label(right)
            return tree(fib_n, [left, right])
>>> fib_tree(5)
[5, [2, [1], [1, [0], [1]]], [3, [1, [0], [1]], [2, [1], [1, [0], [1]]]]]

Python

>>> def count_leaves(tree):
      if is_leaf(tree):
          return 1
      else:
          branch_counts = [count_leaves(b) for b in branches(tree)]
          return sum(branch_counts)
>>> count_leaves(fib_tree(5))
8

Partition trees

Python

>>> def print_parts(tree, partition=[]):
        if is_leaf(tree):
            if label(tree):
                print(' + '.join(partition))
        else:
            left, right = branches(tree)
            m = str(label(tree))
            print_parts(left, partition + [m])
            print_parts(right, partition)

>>> print_parts(partition_tree(6, 4))
4 + 2
4 + 1 + 1
3 + 3
3 + 2 + 1
3 + 1 + 1 + 1
2 + 2 + 2
2 + 2 + 1 + 1
2 + 1 + 1 + 1 + 1
1 + 1 + 1 + 1 + 1 + 1

2.3.7 链表 ¶

linked list
abstract data representation

Python

>>> def partitions(n, m):
"""返回一个包含 n 的分割方案的链表，其中每个正整数不超过 m"""
if n == 0:
    return link(empty, empty) # 包含空分割的链表
elif n < 0 or m == 0:
    return empty
else:
    using_m = partitions(n-m, m)
    with_m = apply_to_all_link(lambda s: link(m, s), using_m)
    without_m = partitions(n, m-1)
    return extend_link(with_m, without_m)

>>> def print_partitions(n, m):
        lists = partitions(n, m)
        strings = apply_to_all_link(lambda s: join_link(s, " + "), lists)
        print(join_link(strings, "\n"))

>>> print_partitions(6, 4)
4 + 2
4 + 1 + 1
3 + 3
3 + 2 + 1
3 + 1 + 1 + 1
2 + 2 + 2
2 + 2 + 1 + 1
2 + 1 + 1 + 1 + 1
1 + 1 + 1 + 1 + 1 + 1

2.4 可变数据 ¶

object-oriented programming

2.4.1 对象隐喻 ¶

attributes
method

2.4.2 序列对象 ¶

mutable
Sharing and Identity
列表推导式:

Python

>>> from unicodedata import lookup
>>> [lookup('WHITE ' + s.upper() + ' SUIT') for s in suits]
['♡', '♢', '♤', '♧']

tuple

2.4.3 字典 ¶

key-value pairs

2.4.4 局部状态 ¶

local state

Python

>>> def make_withdraw(balance):
"""返回一个每次调用都会减少 balance 的 withdraw 函数"""
def withdraw(amount):
    nonlocal balance                 # 声明 balance 是非局部的
    if amount > balance:
        return '余额不足'
    balance = balance - amount       # 重新绑定
    return balance
return withdraw

Python Particulars

2.4.5 非局部 Non-local 赋值的好处 ¶

这样，每个 withdraw 实例都保持自己的 balance 状态，但程序中的任何其他函数都无法访问该状态。从更高的层面来看这种情况，我们抽象了一个银行账户，它自己管理自己的状态，其行为方式与世界上所有其它账户一样：随着时间推移，账户的状态会根据账户的取款记录而发生变化。

2.4.6 非局部 Non-local 赋值的代价 ¶

正确理解包含 nonlocal 声明的代码的关键是记住：只有函数调用才能引入新帧。赋值语句只能更改现有帧中的绑定关系。在这种情况下，除非 make_withdraw 被调用两次，否则只能有一个 balance 绑定。
Sameness and change
referentially transparent

2.4.7 列表和字典实现 ¶

函数是一个 dispatch （调度）函数，其参数首先是一个期望的指令，代表期望这个函数做什么；然后是该方法的需要用到的参数。此指令是一个字符串，用于命名函数应执行的操作。可以将这个 dispatch 函数理解为多个不同函数的抽象：第一个参数确定目标函数的行为，并为该行为入参其他参数。
用字符串也太逆天了。

Python

>>> def mutable_link():
"""返回一个可变链表的函数"""
contents = empty
def dispatch(message, value=None):
    nonlocal contents
    if message == 'len':
        return len_link(contents)
    elif message == 'getitem':
        return getitem_link(contents, value)
    elif message == 'push_first':
        contents = link(value, contents)
    elif message == 'pop_first':
        f = first(contents)
        contents = rest(contents)
        return f
    elif message == 'str':
        return join_link(contents, ", ")
return dispatch

>>> def to_mutable_link(source):
"""返回一个与原列表相同内容的函数列表"""
s = mutable_link()
for element in reversed(source):
    s('push_first', element)
return s

>>> s = to_mutable_link(suits)
>>> type(s)
<class 'function'>
>>> print(s('str'))
heart, diamond, spade, club

字典实现 :

Python

>>> def dictionary():
"""返回一个字典的函数实现"""
records = []
def getitem(key):
    matches = [r for r in records if r[0] == key]
    if len(matches) == 1:
        key, value = matches[0]
        return value
def setitem(key, value):
    nonlocal records
    non_matches = [r for r in records if r[0] != key]
    records = non_matches + [[key, value]]
def dispatch(message, key=None, value=None):
    if message == 'getitem':
        return getitem(key)
    elif message == 'setitem':
        setitem(key, value)
return dispatch

2.4.8 调度字典（Dispatch Dictionaries）¶

用字典存储消息。

Python

def account(initial_balance):
    def deposit(amount):
        dispatch['balance'] += amount
        return dispatch['balance']
    def withdraw(amount):
        if amount > dispatch['balance']:
            return 'Insufficient funds'
        dispatch['balance'] -= amount
        return dispatch['balance']
    dispatch = {'deposit':   deposit,
                'withdraw':  withdraw,
                'balance':   initial_balance}
    return dispatch

def withdraw(account, amount):
    return account['withdraw'](amount)
def deposit(account, amount):
    return account['deposit'](amount)
def check_balance(account):
    return account['balance']

a = account(20)
deposit(a, 5)
withdraw(a, 17)
check_balance(a)

2.4.9 约束传递 (Propagating Constraints) ¶

connector
Using the Constraint System

Python

>>> celsius = connector('Celsius')
>>> fahrenheit = connector('Fahrenheit')
>>> def converter(c, f):
    """用约束条件连接 c 到 f，将摄氏度转换为华氏度."""
    u, v, w, x, y = [connector() for _ in range(5)]
    multiplier(c, w, u)
    multiplier(v, x, u)
    adder(v, y, f)
    constant(w, 9)
    constant(x, 5)
    constant(y, 32)
>>> converter(celsius, fahrenheit)

>>> celsius['set_val']('user', 25)
Celsius = 25
Fahrenheit = 77.0

>>> fahrenheit['set_val']('user', 212)
Contradiction detected: 77.0 vs 212

>>> celsius['forget']('user')
Celsius is forgotten
Fahrenheit is forgotten

>>> fahrenheit['set_val']('user', 212)
Fahrenheit = 212
Celsius = 100.0

# Implementing the Constraint System
>>> connector ['set_val'](source, value)  """表示 source 在请求连接器将当前值设为 value"""
>>> connector ['has_val']()  """返回连接器是否已经具有值"""
>>> connector ['val']  """是连接器的当前值"""
>>> connector ['forget'](source)  """告诉连接器 source 请求遗忘它的值"""
>>> connector ['connect'](source)  """告诉连接器参与新的约束，即 source"""
>>> constraint['new_val']()  """表示与约束相连的某个连接器具有新的值。"""
>>> constraint['forget']()  """表示与约束相连的某个连接器遗忘了值。"""

>>> from operator import add, sub
>>> def adder(a, b, c):
        """约束 a+b=c"""
        return make_ternary_constraint(a, b, c, add, sub, sub)

>>> def make_ternary_constraint(a, b, c, ab, ca, cb):
    """约束 ab(a,b)=c，ca(c,a)=b，cb(c,b)=a"""
    def new_value():
        av, bv, cv = [connector['has_val']() for connector in (a, b, c)]
        if av and bv:
            c['set_val'](constraint, ab(a['val'], b['val']))
        elif av and cv:
            b['set_val'](constraint, ca(c['val'], a['val']))
        elif bv and cv:
            a['set_val'](constraint, cb(c['val'], b['val']))
    def forget_value():
        for connector in (a, b, c):
            connector['forget'](constraint)
    constraint = {'new_val': new_value, 'forget': forget_value}
    for connector in (a, b, c):
        connector['connect'](constraint)
    return constraint

>>> from operator import mul, truediv
>>> def multiplier(a, b, c):
        """约束 a*b=c"""
        return make_ternary_constraint(a, b, c, mul, truediv, truediv)

>>> def constant(connector, value):
    """常量赋值"""
    constraint = {}
    connector['set_val'](constraint, value)
    return constraint

# Representing connectors
>>> def connector(name=None):
    """限制条件之间的连接器"""
    informant = None
    constraints = []
    def set_value(source, value):
        nonlocal informant
        val = connector['val']
        if val is None:
            informant, connector['val'] = source, value
            if name is not None:
                print(name, '=', value)
            inform_all_except(source, 'new_val', constraints)
        else:
            if val != value:
                print('Contradiction detected:', val, 'vs', value)
    def forget_value(source):
        nonlocal informant
        if informant == source:
            informant, connector['val'] = None, None
            if name is not None:
                print(name, 'is forgotten')
            inform_all_except(source, 'forget', constraints)
    connector = {'val': None,
                 'set_val': set_value,
                 'forget': forget_value,
                 'has_val': lambda: connector['val'] is not None,
                 'connect': lambda source: constraints.append(source)}
    return connector

>>> def inform_all_except(source, message, constraints):
    """告知信息除了 source 外的所有约束条件"""
    for c in constraints:
        if c != source:
            c[message]()

2.5 面向对象编程 ¶

object
dot notation
class

2.5.1 对象和类 ¶

2.5.2 类的定义 ¶

__init__ 类的构造函数（constructor）

Python

>>> class Account:
        def __init__(self, account_holder):
            self.balance = 0
            self.holder = account_holder
        def deposit(self, amount):
            self.balance = self.balance + amount
            return self.balance
        def withdraw(self, amount):
            if amount > self.balance:
                return 'Insufficient funds'
            self.balance = self.balance - amount
            return self.balance

2.5.3 消息传递和点表达式 ¶

Python

>>> getattr(spock_account, 'balance')
10
>>> hasattr(spock_account, 'deposit')
True


>>> type(Account.deposit)
<class 'Function'>
>>> type(spock_account.deposit)
<class 'method'>
# 为类的属性，方法只是一个函数，但作为实例的属性，它是一个绑定方法

>>> Account.deposit(spock_account, 1001)    # 函数 deposit 接受两个参数
1011
>>> spock_account.deposit(1000)             # 方法 deposit 接受一个参数
2011

命名约定：类名通常使用 CapWords 约定（也称为 CamelCase，因为名称中间的大写字母看起来像驼峰）编写。方法名称遵循使用下划线分隔的小写单词命名函数的标准约定。

在某些情况下，有一些实例变量和方法与对象的维护和一致性相关，我们不希望对象的用户看到或使用。它们不是类定义的抽象的一部分，而是实现的一部分。Python 的约定规定，如果属性名称以下划线开头，则只能在类本身的方法中访问它，而不是用户访问。

2.5.4 类属性 ¶

感觉没什么用 :

Python

>>> Account.interest = 0.05     # 改变类属性
>>> spock_account.interest      # 实例属性发生变化（该实例中没有和类属性同名称的实例属性）
0.05
>>> kirk_account.interest       # 如果实例中存在和类属性同名的实例属性，则改变类属性，不会影响实例属性
0.08

2.5.5 继承 ¶

base class
- parent class
- super class
subcladd
- child class

2.5.6 使用继承 ¶

Python

>>> class Account:
        """一个余额非零的账户。"""
        interest = 0.02
        def __init__(self, account_holder):
            self.balance = 0
            self.holder = account_holder
        def deposit(self, amount):
            """存入账户 amount，并返回变化后的余额"""
            self.balance = self.balance + amount
            return self.balance
        def withdraw(self, amount):
            """从账号中取出 amount，并返回变化后的余额"""
            if amount > self.balance:
                return 'Insufficient funds'
            self.balance = self.balance - amount
            return self.balance

>>> class CheckingAccount(Account):
        """从账号取钱会扣出手续费的账号"""
           withdraw_charge = 1
           interest = 0.01
           def withdraw(self, amount):
                 return Account.withdraw(self, amount + self.withdraw_charge)

接口

Python

>>> def deposit_all(winners, amount=5):
        for account in winners:
            account.deposit(amount)         # 这里调用的是实例 account 的 deposit 方法
            # 对于不同实例来说，它们的 deposit 方法可能不同。这个例子相对于下面来讲，更加具有健壮性

2.5.7 多继承 ¶

继承排序问题没有正确的解决方案，因为在某些情况下，我们可能更愿意将某些继承类置于其他类之上。但是，任何支持多重继承的编程语言都必须以一致的方式选择某些排序，以便该语言的用户可以预测其程序的行为。

进一步阅读。Python 使用称为 C3 方法解析排序的递归算法解析此名称。可以在所有类上使用 mro 方法查询任何类的方法解析顺序。

Python

>>> [c.__name__ for c in AsSeenOnTVAccount.mro()]
['AsSeenOnTVAccount', 'CheckingAccount', 'SavingsAccount', 'Account', 'object']

2.5.8 对象的作用 ¶

另一方面，类可能不是实现某些抽象的最佳机制。函数式抽象提供了一个更自然的隐喻来表示输入和输出之间的关系。我们不应该觉得必须将程序中的每一点逻辑都塞进一个类中，尤其是在定义独立函数来操作数据更自然的情况下。函数还可以强制实现关注点的分离。换句话说，函数式编程提供了另一种有效地组织程序逻辑的方法，使得程序员能够更好地处理和维护程序。在某些情况下，使用函数式编程方法可能比使用面向对象编程更自然和有效。

2.6 实现类和对象 ¶

object-oriented programming paradigm
即使在没有内置对象系统的编程语言中，程序也可以是面向对象的。
放弃点表示法->调度字典实现消息传递

2.6.1 实例 ¶

Python

>>> def make_instance(cls):
    """Return a new object instance, which is a dispatch dictionary."""
    def get_value(name):
        if name in attributes:
            return attributes[name]
        else:
            value = cls['get'](name)
            return bind_method(value, instance)
    def set_value(name, value):
        attributes[name] = value
    attributes = {}
    instance = {'get': get_value, 'set': set_value}
    return instance

>>> def bind_method(value, instance):
    """Return a bound method if value is callable, or value otherwise."""
    if callable(value):
        def method(*args):
            return value(instance, *args)
        return method
    else:
        return value

2.6.2 类 ¶

Python

>>> def make_class(attributes, base_class=None):
    """Return a new class, which is a dispatch dictionary."""
    def get_value(name):
        if name in attributes:
            return attributes[name]
        elif base_class is not None:
            return base_class['get'](name)
    def set_value(name, value):
        attributes[name] = value
    def new(*args):
        return init_instance(cls, *args)
    cls = {'get': get_value, 'set': set_value, 'new': new}
    return cls

>>> def init_instance(cls, *args):
    """Return a new object with type cls, initialized with args."""
    instance = make_instance(cls)
    init = cls['get']('__init__')
    if init:
        init(instance, *args)
    return instance

3 计算机程序的解释 ¶

3.1 引言 ¶

许多解释器都有一个优雅的结构，即两个互递归函数：

第一个函数求解环境中的表达式
第二个函数将函数应用于参数

3.2 函数式编程 ¶

只使用表达式而不使用语句，特别适合符号计算
处理的数据都是不可变的（immutable）

Python

(if <predicate> <consequent> <alternative>)

(define pi 3.14)
(* pi 3.14)

(define (<name> <formal parameters>) <body>)
eg1:
    (define (average x y)
      (/ (+ x y) 2))
eg2:
    (define (abs x)
    (if (< x 0)
        (- x)
        x))
eg3:
    (define (sqrt x)
      (define (good-enough? guess)
        (< (abs (- (square guess) x)) 0.001))
      (define (improve guess)
        (average guess (/ x guess)))
      (define (sqrt-iter guess)
        (if (good-enough? guess)
            guess
            (sqrt-iter (improve guess))))
      (sqrt-iter 1.0))
    (sqrt 9)

(lambda (<formal-parameters>) <body>)
eg1:
    (define (plus4 x) (+ x 4))
    (define plus4 (lambda (x) (+ x 4))) # both are OK

# 特殊的值 nil 或 '() 表示空列表

# null? 谓词的使用:
    (define (length items)
      (if (null? items)
          0
          (+ 1 (length (cdr items)))))
    (define (getitem items n)
      (if (= n 0)
          (car items)
          (getitem (cdr items) (- n 1))))
    (define squares (list 1 4 9 16 25))

    (length squares)

    (getitem squares 3)

# 任何不被求值的表达式都被称为被引用
    (list 'define 'list)

# turtle使用+递归画图

3.3 异常 ¶

raise
assert

Python

>>> raise Exception(' An error occurred')
Traceback (most recent call last):
    File "<stdin>", line 1, in <module>
Exception: an error occurred

raising an exception
- read-eval-print-loop 即 REPL
- stack backtrace
handling exceptions

Python

try
    <try suite>
except <exception class> as <name>:
    <except suite>

异常是个类，可以有额外的属性，可以避免报错，让程序给出一个较为粗糙的值：

Python

>>> class IterImproveError(Exception):
        def __init__(self, last_guess):
            self.last_guess = last_guess
>>> def improve(update, done, guess=1, max_updates=1000):
        k = 0
        try:
            while not done(guess) and k < max_updates:
                guess = update(guess)
                k = k + 1
            return guess
        except ValueError:
            raise IterImproveError(guess)
>>> def find_zero(f, guess=1):
        def done(x):
            return f(x) == 0
        try:
            return improve(newton_update(f), done, guess)
        except IterImproveError as e:
            return e.last_guess
>>> from math import sqrt
>>> find_zero(lambda x: 2*x*x + sqrt(x))
-0.030211203830201594

3.4 组合语言的解释器 ¶

计算器语言 -> 简略解释器
scheme 对
- pair
- nil
表达式树
解析表达式树
- 词法分析器（lexical analyzer）/ 分词器（tokenizer）
  - 标记（token）
- 语法分析器（syntactic analyzer）
  - 数字和调用表达式
    讲了一下计算器解释器交互式页面的表达式如何计算和异常处理

3.5 抽象语言的解释器 ¶

扩展 scheme_reader 解析点列表和引号
求值（Evaluation）
函数应用（Procedure application）
求值 / 应用递归
数据即程序

4 数据处理 ¶

4.1 引言 ¶

pipelines
sequence interface
unbounded

4.2 隐式序列 ¶

我们只在有需要的时候才计算元素
Lazy computation

4.2.1 迭代器 ¶

两个组件 :

检索下一个元素的机制
到达序列末尾并且没有剩余元素，发出信号的机制

Python

>>> next(iterator)
7
>>> next(iterator)
Traceback (most recent call las):
  File "<stdin>", line 1, in <module>
StopIteration

>>> try:
        next(iterator)
    except StopIteration:
        print('No more values')
No more values

4.2.2 可迭代性 ¶

iterable value
可迭代对象:

序列值 : string & tuples
容器 : sets & Dictionaries