深入理解计算机系统 ¶
约 997 个字 36 行代码 14 张图片 预计阅读时间 5 分钟 共被读过 次
1 计算机系统漫游 ¶
2 信息的表示和处理 ¶
- 把位组合再一起，再加上 interpretation
- 三种重要的数字表示
- unsigned
- two's-complement
- floating-point
- overflow
- 浮点数是近似的
2.1 信息存储 ¶
- 1 byte = 8 bits
- virtual memory
- address
- virtual address space
- 讲存储器空间划分为更可管理的单元，来存放不同的 program object
2.1.1 十六进制表示法 ¶
- 0x...
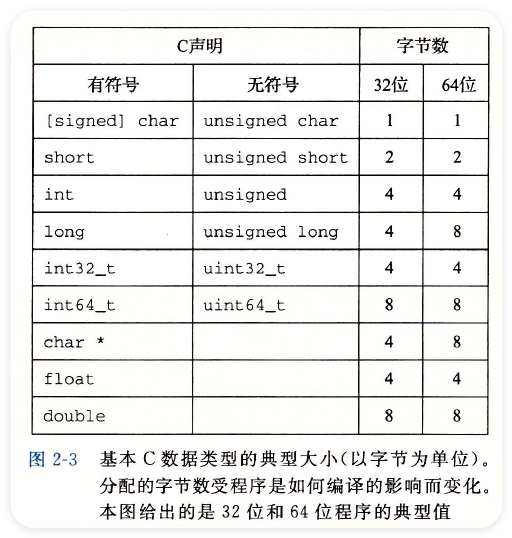
2.1.2 字数据大小 ¶
- word size
- nominal size
- 字长决定的最重要的系统参数就是虚拟地址空间的最大大小
- 字长为 \(\displaystyle \omega\) 为的机器，虚拟地址的范围为 \(\displaystyle 0\sim2^{\omega} - 1\)
- 大多数 64 位机器可以运行 32 位机器编译的程序，即向后兼容
- 为了避免大小和不同编译器设置带来的奇怪行为，我们有了 int 32_t 和 int 64_t
- C 语言对声明的关键词顺序不敏感
2.1.3 寻址和字节顺序 ¶
- 小端编址
- 就是右边放小的，要从右往左读
- 字节顺序变得重要的三种情况
- 网络应用程序的代码编写必须遵守已建立的关于字节顺序的规则
- disassembler
- 编写规避正常的类型系统的程序
- cast or union in C
- 对应用编程不推荐，但是对系统级编程是必需的
C
#include <stdio.h>
typedef unsigned char *byte_pointer;
void show_bytes(byte_pointer start, size_t len) {
size_t i;
for (i = 0; i < len; i++)
printf(" %.2x", start[i]);
printf("\n");
}
void show_int(int x) { show_bytes((byte_pointer)&x, sizeof(int)); }
void show_float(float x) { show_bytes((byte_pointer)&x, sizeof(float)); }
void show_pointer(void *x) { show_bytes((byte_pointer)&x, sizeof(void *)); }
void test_show_bytes(int val) {
int ival = val;
float fval = (float)ival;
int *pval = &ival;
show_int(ival);
show_float(fval);
show_pointer(pval);
}
int main() {
int val = 12345;
test_show_bytes(val);
return 0;
}
2.1.4 表示字符串 ¶
2.1.5 表示代码 ¶
- 二进制代码很少能在不同机器和操作系统组合之间移植
2.1.6 布尔代数简介 ¶
- 可以扩展到位向量的运算
- 布尔代数
- Boolean ring
- additive inverse
- 和集合的对应
2.1.7 C 语言中的位级运算 ¶
- 掩码运算
2.1.8 C 语言中的逻辑运算 ¶
2.1.9 C 语言中的移位运算 ¶
- 逻辑右移
- 算数右移
- 实际上，几乎所有的编译器都对有符号数使用算术右移，而对于无符号数，右移必须是逻辑的（C 语言）
- 而对于 Java
x>>k是算数右移，x>>>k是逻辑右移 - 对于 C 语言，移动 \(\displaystyle k \text{ mod } \omega\)
- 加减的优先级比移位算法要搞
2.2 整数表示 ¶
2.2.1 整型数据类型 ¶
- 64 位和 32 位是不一样的
- 取值范围不是对称的
- Java 只支持有符号数
2.2.2 无符号数的编码 ¶
- 把向量写成二进制表示的数，就得到了无符号表示
\[ B2U_w(\vec{x})\doteq\sum_{i=0}^{u-1}x_i2^i \]
\[ B2U_w:\{0, 1\}^w\to\{0, \cdots,2^w-1\} \]
- 无符号数编码的唯一性
- \(\displaystyle 函数B2U_w是一个双射。\)
2.2.3 补码编码 ¶
- two's-complement
- negative weight
\[ B2T_w(\vec{x})\doteq- x_{w-1}2^{w-1}+\sum_{i=0}^{w-2}x_i2^i \]
\[ B2T_{w}\colon \{0, 1\}^{w}\to\langle TMin_{w}, \cdots, TMax_{w} \rangle \]
- 补码编码的唯一性
-
\(\displaystyle 函数B2T_w是一个双射。\)
-
反码
\[ B2O_w(\vec{x})\doteq-x_{w-1}(2^{w-1}-1)+\sum_{i=0}^{w-2}x_i2^i \]
- 原码
\[ B2S_w(\vec{x})\doteq(-1)^{x_{w-1}}\cdot\bigl(\sum_{i=0}^{w-2}x_i2^i\bigr) \]
- 对于数字 0 有两种不同的编码方式
2.2.4 有符号数和无符号数之间的转换 ¶
- 保持位值不变，改变解释方式
\[ T2U_{_w}(x)\doteq B2U_{_w}( T2B_{_w}(x) ) \]
- 补码转换为无符号数
\[ T2U_w(x)=\begin{cases}x+2^w,&x<0\\x,&x\geqslant0\end{cases} \]
- 无符号数转换为补码
\[ U2T_w(u)=\begin{cases}u ,&u\leqslant TMax_w\\u-2^w ,&u>TMax_w\end{cases} \]
2.2.5 C 语言中的有符号数与无符号数 ¶
- 一个运算符是有符号的而另一个是无符号的，那 C 程序会把有符号的转换为无符号的。
2.2.6 扩展一个数字的位表示 ¶
- 无符号数的 zero extension
- 补码数的符号扩展
2.2.7 截断数字 ¶
2.2.8 关于有符号数与无符号数的建议 ¶
2.3 整数运算 ¶
2.3.1 无符号加法 ¶
- Lisp 支持无限精度的运算
\[ x+_w^uy=\begin{cases}x+y,&x+y<2^w&\text{正常}\\x+y-2^w,&2^w\leqslant x+y<2^{w+1}&\text{溢出}\end{cases} \]
