统计学习方法 ¶
约 3356 个字 43 张图片 预计阅读时间 17 分钟 共被读过 次
1 统计学习方法概论 ¶
1.1 统计学习 ¶
- 统计学习的特点
- 以计算机及网络为平台
- 以数据为研究对象
- 目的是对数据进行预测与分析
- 交叉学科
- 统计学习的对象
- 是数据
- 统计学习的目的
- 统计学习的方法
- 主要有
- 监督学习(本书主要讨论)
- 非监督学习
- 半监督学习
- 强化学习
- 三要素
- 模型
- 策略
- 算法
- 实现步骤
- 得到一个训练数据集合
- 确定学习模型的集合
- 确定学习的策略
- 确定学习的算法
- 通过学习方法选择最优模型
- 利用学习的最优模型对新数据进行预测或分析
- 主要有
- 统计学习的研究
- 方法
- 理论
- 应用
- 统计学习的重要性
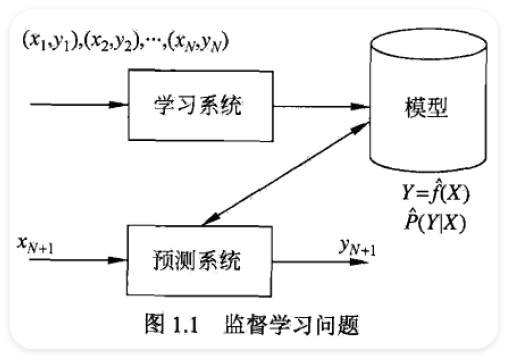
1.2 监督学习 ¶
1.2.1 基本概念 ¶
- 输入空间、特征空间与输出空间
- 每个输入是一个实例,通常由特征向量表示
- 监督学习从训练数据集合中学习模型,对测试数据进行预测
- 根据输入变量和输出变量的不同类型
- 回归问题 : 都连续
- 分类问题 : 输出有限离散
- 标注问题 : 都是变量序列
- 联合概率分布
- 假设空间
- 模型属于由输入空间到输出空间的映射的集合,这个集合就是假设空间
- 模型可以是(非)概率模型
1.2.2 问题的形式化 ¶
1.3 统计学习三要读 ¶
- 方法 = 模型 + 策略 + 算法
1.3.1 模型 ¶
- 模型就是索要学习的条件概率分布或决策函数
\[ \mathcal{F}=\{f\mid Y=f(X)\} \]
- 参数空间
\[ \mathcal{F}=\{f | Y=f_{\theta}(X),\theta\in\mathbf{R}^{n}\} \]
- 同样可以定义为条件概率的集合
\[ \mathcal{F}=\{P|P(Y|X)\} \]
\[ \mathcal{F}=\{P\mid P_{\theta}(Y\mid X),\theta\in\mathbf{R}^{n}\} \]
1.3.2 策略 ¶
- 损失函数和风险函数
- loos function or cost function \(\displaystyle L(Y,f(X))\)
- 0-1 loss function
- \(\displaystyle L(Y,f(X))=\begin{cases}1,&Y\neq f(X)\\0,&Y=f(X)\end{cases}\)
- quadratic loss function
- \(\displaystyle L(Y,f(X))=(Y-f(X))^{2}\)
- absolute loss function
- \(\displaystyle L(Y,f(X))=|Y-f(X)|\)
- logarithmic loss function or log-likelihood loss function
- \(\displaystyle L(Y,P(Y\mid X))=-\log P(Y\mid X)\)
- 0-1 loss function
- \(\displaystyle R_{\exp}(f)=E_{P}[L(Y,f(X))]=\int_{x\times y}L(y,f(x))P(x,y)\mathrm{d}x\mathrm{d}y\)
- risk function or expected loss
- 但是联合分布位置,所以要学习,但是这样以来风险最小又要用到联合分布,那么这就成为了病态问题 (ill-formed problem)
- empirical risk or empirical loss
- \(\displaystyle R_{\mathrm{emp}}(f)=\frac{1}{N}\sum_{i=1}^{N}L(y_{i},f(x_{i}))\)
- 当 \(\displaystyle N\) 趋于无穷时,经验风险趋于期望风险
- 这就关系到两个基本策略 :
- 经验风险最小化
- 结构风险最小化
- 这就关系到两个基本策略 :
- loos function or cost function \(\displaystyle L(Y,f(X))\)
- 经验风险最小化与结构风险最小化
- empirical risk minimization (样本容量比较大的时候)
- \(\displaystyle \min_{f\in\mathcal{F}} \frac{1}{N}\sum_{i=1}^{N}L(y_{i},f(x_{i}))\)
- maximum likelihood estimation
- structural risk minimization
- regularization
- \(\displaystyle R_{\mathrm{sm}}(f)=\frac{1}{N}\sum_{i=1}^{N}L(y_{i},f(x_{i}))+\lambda J(f)\)
- 复杂度表示了对复杂模型的乘法
- maximum posterior probability estimation
- empirical risk minimization (样本容量比较大的时候)
1.3.3 算法 ¶
1.4 模型评估与模型选择 ¶
1.4.1 训练误差与测试误差 ¶
\[ R_{\mathrm{emp}}(\hat{f})=\frac{1}{N}\sum_{i=1}^{N}L(y_{i},\hat{f}(x_{i})) \]
\[ e_{\mathrm{test}}=\frac{1}{N^{\prime}}\sum_{i=1}^{N^{\prime}}L(y_{i},\hat{f}(x_{i})) \]
\[ r_{\mathrm{test}}+e_{\mathrm{test}}=1 \]
- generalization ability
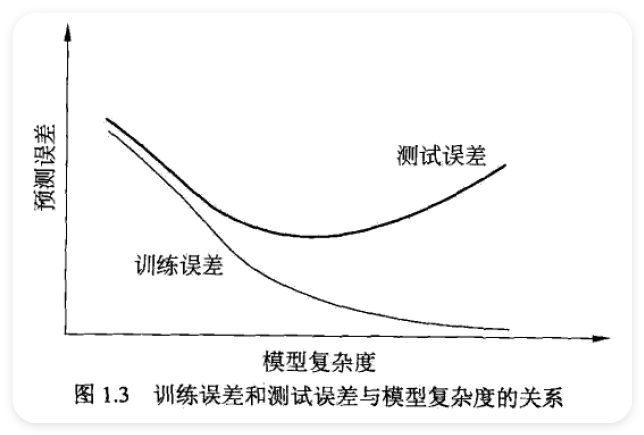
1.4.2 过拟合与模型选择 ¶
1.5 正则化与交叉验证 ¶
1.5.1 正则化 ¶
\[ L(w)=\frac{1}{N}\sum_{i=1}^{N}(f(x_{i};w)-y_{i})^{2}+\frac{\lambda}{2}\parallel w\parallel^{2} \]
1.5.2 交叉验证 ¶
- cross validation
- 数据集
- 训练集
- 验证集
- 测试集 1. 简单交叉验证 2. \(\displaystyle S\) 折交叉验证 3. 留一交叉验证
1.6 泛化能力 ¶
1.6.1 泛化误差 ¶
- generalization error
\[ R_{\exp}(\hat{f})=E_{P}[L(Y,\hat{f}(X))]=\int_{R\times y}L(y,\hat{f}(x))P(x,y)\mathrm{d}x\mathrm{d}y \]
1.6.2 泛化误差上界 ¶
1.7 生成模型与判别模型 ¶
- generative model
- 还原出联合概率分布 \(\displaystyle P(X,Y)\)
- 朴素贝叶斯法
- 隐马尔可夫模型
- 收敛速度快
- discriminative model
- 直接学习决策函数或条件概率分布 \(\displaystyle P(Y|X)\)
- \(\displaystyle k\) 近邻法
- 感知机
- 决策树
- 逻辑斯谛回归模型
- 最大熵模型
- 支持向量机
- 提升方法
- 条件随机场
- 准确度高
1.8 分类问题 ¶
\[ \frac{2}{F_{1}}=\frac{1}{P}+\frac{1}{R} \]
\[ F_{1}=\frac{2TP}{2TP+FP+FN} \]
- text classification
1.9 标注问题 ¶
- tagging 是 classificationd 一个推广
- 是 structure prediction 的简单形式
- 隐马尔可夫模型
- 条件随机场
1.10 回归问题 ¶
- regression
- (非)线性回归,一元回归,多元回归
2 感知机 ¶
- perception
- 感知机对应于输入空间中将实例划分成正负两类的分离超平面,属于判别模型
- 原始形式和对偶形式
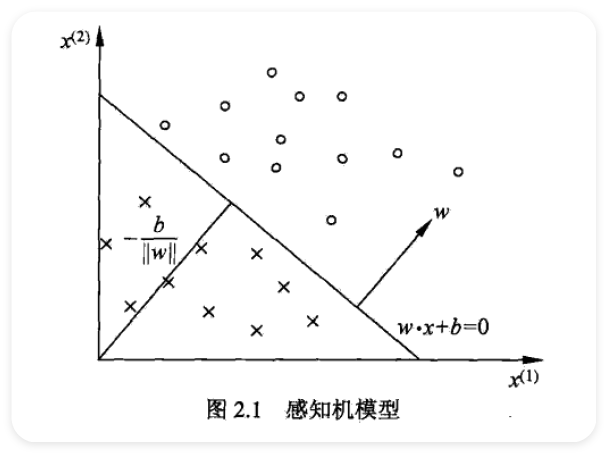
2.1 感知机模型 ¶
- 假设空间是定义在特征空间中所有的线性分类模型(linear classification model)\(\displaystyle \{f|f(x) = w \cdot x+b\}\)
- separating hyperplane
2.2 感知机学习策略 ¶
2.2.1 数据集的线性可分性 ¶
2.2.2 感知机学习策略 ¶
- 定义损失函数并将损失函数极小化
\[ L(w,b)=-\sum_{x_{i}\in M}y_{i}(w\cdot x_{i}+b) \]
2.2.3 感知机学习算法 ¶
2.2.4 感知机学习算法的原始形式 ¶
\[ \min_{w,b}L(w,b)=-\sum_{x_{i}\in M}y_{i}(w\cdot x_{i}+b) \]
- stochastic gradient descent
\[ \nabla_{_w}L(w,b)=-\sum_{x_{i}\in M}y_{i}x_{i} \]
\[ \nabla_{b}L(w,b)=-\sum_{x_{i}eM}y_{i} \]
\[ w\leftarrow w+\eta y_{i}x_{i} \]
\[ b\leftarrow b+\eta y_{i} \]
2.2.5 算法的收敛性 ¶
- 为了得到唯一的超平面,需要对分离超平面增加约束条件,即线性支持向量机
- 如果训练集线性不可分,那么感知机学习算法不收敛
2.2.6 感知机学习算法的对偶形式 ¶
\[ \begin{aligned}&w\leftarrow w+\eta y_{i}x_{i}\\&b\leftarrow b+\eta y_{i}\end{aligned} \]
\[ w=\sum_{i=1}^{N}\alpha_{i}y_{i}x_{i} \]
\[ b=\sum_{i=1}^{N}\alpha_{i}y_{i} \]
- Gram matrix
\[ G=[x_{i}\cdot x_{j}]_{N\times N} \]
3 \(\displaystyle k\) 近邻法 ¶
- k-nearest neighbor
3.1 \(\displaystyle k\) 近邻算法 ¶
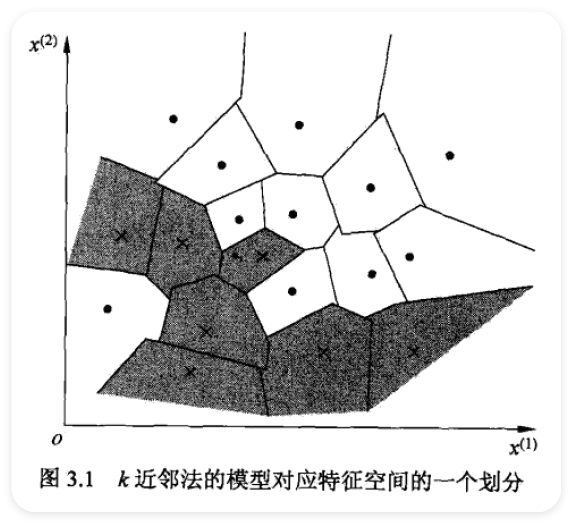
3.2 \(\displaystyle k\) 近邻模型 ¶
3.2.1 模型 ¶
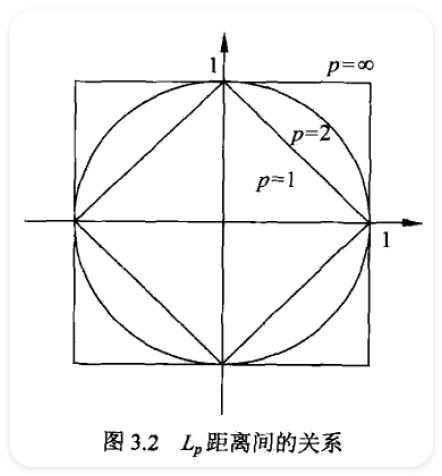
3.3 距离度量 ¶
- \(\displaystyle L_{p}\) distance or Minkowski distamce
- \(\displaystyle L_{p}(x_{i},x_{j})=\left(\sum_{l=1}^{n}\mid x_{i}^{(l)}-x_{j}^{(l)}\mid^{p}\right)^{\frac{1}{p}}\)
- \(\displaystyle L_{2}(x_{i},x_{j})=\left(\sum_{i=1}^{n}\mid x_{i}^{(l)}-x_{j}^{(l)}\mid^{2}\right)^{\frac{1}{2}}\)
- \(\displaystyle L_{1}(x_{i}, x_{j})=\sum_{l=1}^{n}\mid x_{i}^{(l)}-x_{j}^{(l)}\mid\)
- \(\displaystyle L_{\infty}(x_{i}, x_{j})=\max_{l}\mid x_{i}^{(l)}-x_{j}^{(l)}\mid\)
3.3.1 \(\displaystyle k\) 值的选择 ¶
- if k is small, then the approximation error will reduce
- estimation error
- \(\displaystyle k\) 值的减小就意味着整体模型变得复杂,容易发生过拟合
- 在应用中 , \(\displaystyle k\) 值一般取一个比较小的数值,通常采用交叉验证法来选取最优的 \(\displaystyle k\) 值
3.3.2 分类决策规则 ¶
3.4 \(\displaystyle k\) 近邻法的实现 : \(\displaystyle kd\) 树 ¶
- linear scan
- kd tree
3.4.1 构造 \(\displaystyle kd\) 树 ¶
- \(\displaystyle kd\) 树是一二叉树,表示对 \(\displaystyle k\) 维空间的一个划分(partition)
- 通常选择训练实例点在选定坐标轴上的中位数为切分点,虽然这样得到的树是平衡的,但效率未必是最优的


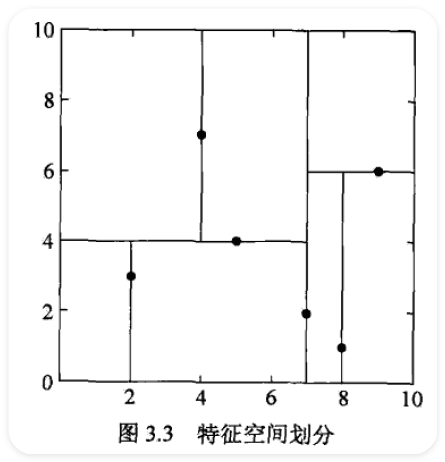
有意思
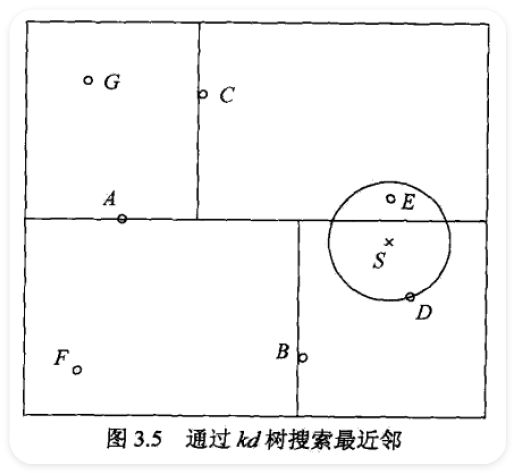
3.4.2 搜索 \(\displaystyle kd\) 树 ¶
4 朴素贝叶斯法 ¶
- 基于贝叶斯定理与特征条件独立假设的分类方法
4.1 朴素贝叶斯法的学习与分类 ¶
4.1.1 基本方法 ¶
- 学习先验概率分布和条件概率分布于是学习到联合概率分布
\[ P(X=x\mid Y=c_{k})=P(X^{(1)}=x^{(1)},\cdots,X^{(n)}=x^{(n)}\mid Y=c_{k}),\quad k=1,2,\cdots,K \]
- 引入了条件独立性假设
\[ \begin{aligned} P(X=x|Y=c_{k})& =P(X^{(1)}=x^{(1)},\cdots,X^{(n)}=x^{(n)}\mid Y=c_{k}) \\ &=\prod_{j=1}^{n}P(X^{(j)}=x^{(j)}\mid Y=c_{k}) \end{aligned} \]
\[ P(Y=c_{k}\mid X=x)=\frac{P(X=x\mid Y=c_{k})P(Y=c_{k})}{\sum_{k}P(X=x\mid Y=c_{k})P(Y=c_{k})} \]
\[ P(Y=c_{k}\mid X=x)=\frac{P(Y=c_{k})\prod_{j}P(X^{(j)}=x^{(j)}\mid Y=c_{k})}{\sum_{k}P(Y=c_{k})\prod_{j}P(X^{(j)}=x^{(j)}\mid Y=c_{k})},\quad k=1,2,\cdots,K \]
\[ y=f(x)=\arg\max_{c_{k}}\frac{P(Y=c_{k})\prod_{j}P(X^{(j)}=x^{(j)}\mid Y=c_{k})}{\sum_{k}P(Y=c_{k})\prod_{j}P(X^{(j)}=x^{(j)}\mid Y=c_{k})} \]
\[ y=\arg\max_{c_{k}}P(Y=c_{k})\prod_{j}P(X^{(j)}=x^{(j)}\mid Y=c_{k}) \]
4.1.2 后验概率最大化的含义 ¶
\[ L(Y,f(X))=\begin{cases}1,&Y\neq f(X)\\0,&Y=f(X)\end{cases} \]
\[ R_{\exp}(f)=E[L(Y,f(X))] \]
\[ R_{\exp}(f)=E_{\chi}\sum_{k=1}^{K}[L(c_{k},f(X))]P(c_{k}\mid X) \]
\[ \begin{align} f(x) &=\arg\min_{y\in\mathcal{Y}}\sum_{k=1}^{K}L(c_{k},y)P(c_{k}\mid X=x) \\ &=\arg\min_{y\in\mathcal{Y}}\sum_{k=1}^{K}P(y\neq c_{k}\mid X=x) \\ &=\arg\min_{y\in\mathcal{Y}}(1-P(y=c_{k}\mid X=x)) \\ &=\arg\max_{y\in\mathcal{Y}}P(y=c_{k}\mid X=x) \end{align} \]
\[ f(x)=\arg\max_{c_{k}}P(c_{k}\mid X=x) \]
- 期望风险最小化准则就得到联考后验概率最大化准则
4.2 朴素贝叶斯法的参数估计 ¶
4.2.1 极大似然估计 ¶
\[ P(Y=c_{k})=\frac{\sum_{i=1}^{N}I(y_{i}=c_{k})}{N} , k=1,2,\cdots,K \]
\[ P(X^{(j)}=a_{ji}\mid Y=c_{k})=\frac{\sum_{i=1}^{N}I(x_{i}^{(j)}=a_{ji},y_{i}=c_{k})}{\sum_{i=1}^{N}I(y_{i}=c_{k})}\\j=1,2,\cdots,n ;\quad l=1,2,\cdots,S_{j} ;\quad k=1,2,\cdots,K \]
4.2.2 学习与分类算法 ¶
4.2.3 贝叶斯估计 ¶
- 极大似然估计可能会出现所要估计的概率值为 0 的情况
- 条件概率的贝叶斯估计
\[ P_{\lambda}(X^{(j)}=a_{ji}\mid Y=c_{k})=\frac{\sum_{i=1}^{N}I(x_{i}^{(j)}=a_{ji},y_{i}=c_{k})+\lambda}{\sum_{i=1}^{N}I(y_{i}=c_{k})+S_{j}\lambda} \]
- when \(\displaystyle \lambda = 0\), it's called Laplace smoothing
\[ \begin{aligned}&P_{\lambda}(X^{(j)}=a_{jl}\mid Y=c_{k})>0\\&\sum_{l=1}^{s_{j}}P(X^{(j)}=a_{jl}\mid Y=c_{k})=1\end{aligned} \]
- 表明贝叶斯估计确实是一种概率分布
- 先验概率的贝叶斯估计
\[ P_{\lambda}(Y=c_{k})=\frac{\sum_{i=1}^{N}I(y_{i}=c_{k})+\lambda}{N+K\lambda} \]
5 决策树 ¶
- decision tree
- 特征选择
- 决策树的生成
- 决策树的修剪
5.1 决策树模型与学习 ¶
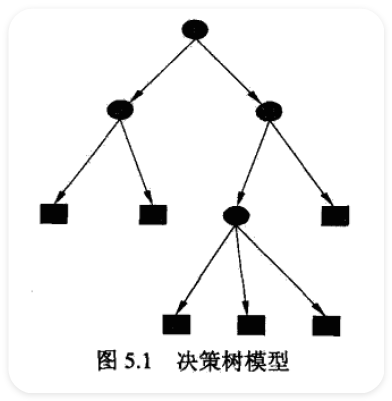
5.1.1 决策树模型 ¶
5.1.2 决策树与 if-then 规则 ¶
- 互斥且完备
- 每一个实例都被一条路径会规则所覆盖,而且只被一条路径或一条规则所覆盖
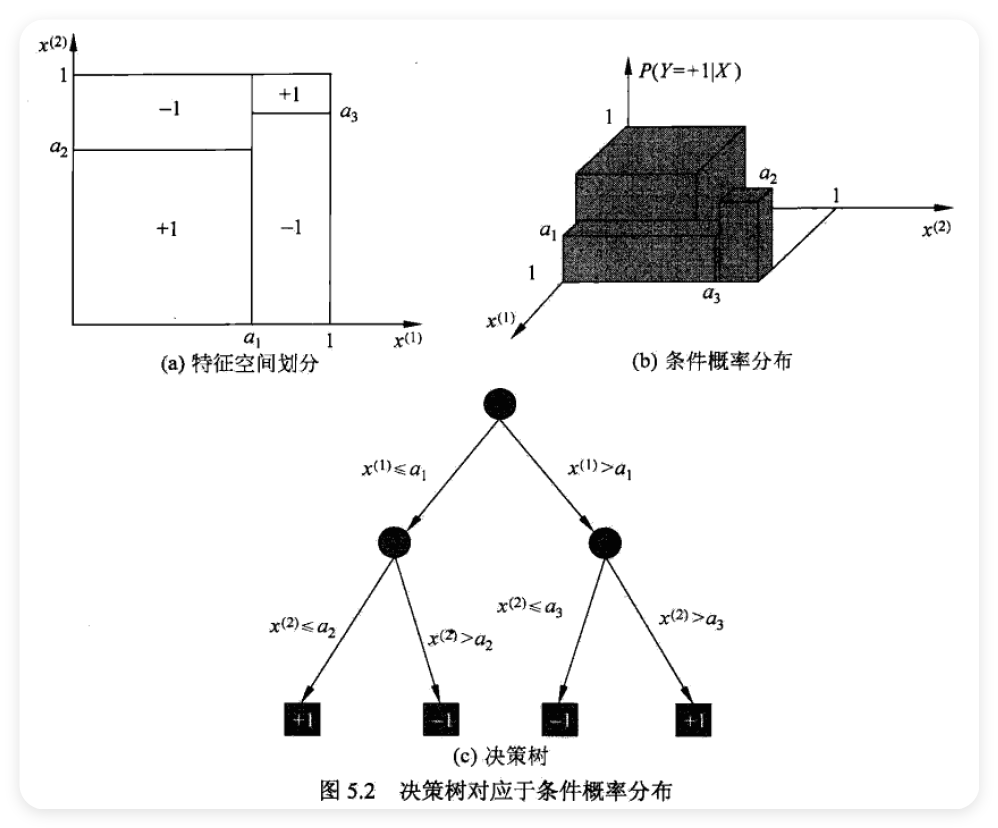
5.1.3 决策树与条件概率分布 ¶
5.1.4 决策树学习 ¶
- 决策树学习本质上是从训练数据集中归纳出一组分类规则
- 在损失函数意义下选择最优决策树的问题,是 NP 完全问题,采用启发式方法,近似求解,这样得到的决策树是次最优(sub-optimal)
- 为了防止过拟合,我们需要对已生成的树自上而下进行剪枝
- 决策树的生成值考虑局部最优,剪枝则考虑全局最优
5.2 特征选择 ¶
5.2.1 特征选择问题 ¶
- 通常特征选择的准则是信息增益或信息增益比
- information gain
5.2.2 信息增益 ¶
- 熵和条件熵
\[ P(X=x_{i})=p_{i} ,\quad i=1,2,\cdots,n \]
\[ H(X)=-\sum_{i=1}^{n}p_{i}\log p_{i} \]
\[ H(p)=-\sum_{i=1}^{n}p_{i}\log p_{i} \]
\[ 0\leqslant H(p)\leqslant\log n \]
\[ P(X=x_{i},Y=y_{j})=p_{ij} ,\quad i=1,2,\cdots,n ;\quad j=1,2,\cdots,m \]
\[ H(Y\mid X)=\sum_{i=1}^{n}p_{i}H(Y\mid X=x_{i}) \]
5.2.3 信息增益比 ¶
5.3 决策树的生成 ¶
5.3.1 ID 3 算法 ¶
- ID 3 算法只有树的生成,所以该算法生成的树容易产生过拟合
5.3.2 C 4.5 的生成算法 ¶
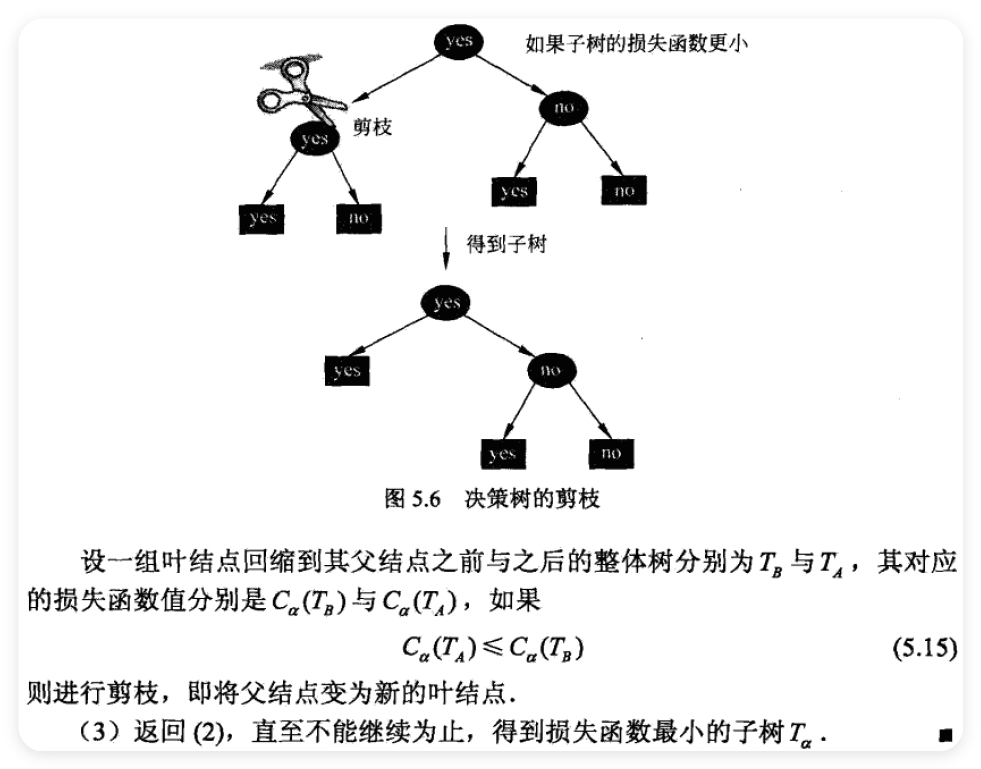
5.4 决策树的剪枝 ¶
- pruning
\[ C_{\alpha}(T)=\sum_{t=1}^{|T|}N_{t}H_{t}(T)+\alpha|T| \]
\[ H_{t}(T)=-\sum_{k}\frac{N_{ik}}{N_{t}}\log\frac{N_{ik}}{N_{t}} \]
\[ C(T)=\sum_{t=1}^{|T|}N_{t}H_{t}(T)=-\sum_{t=1}^{|T|}\sum_{k=1}^{K}N_{tk}\log\frac{N_{tk}}{N_{t}} \]
\[ C_{\alpha}(T)=C(T)+\alpha|T| \]
5.5 CART 算法 ¶
- 分裂与回归树(classification and regression tree)
5.5.1 CART 生成 ¶
- 对回归树用平方误差最小化准则
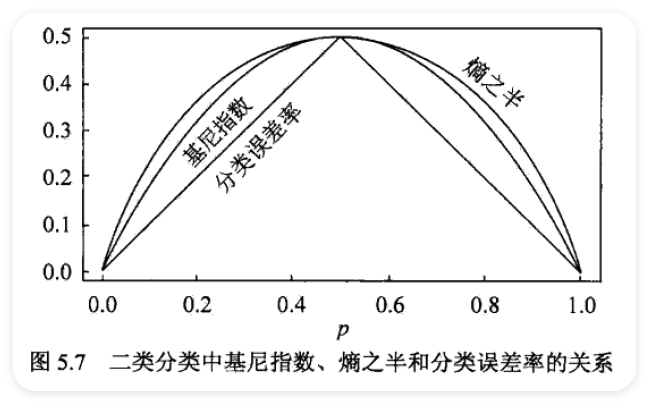
- 对分类树用基尼指数(Gini index)最小化准则 1. 回归树的生成
\[ f(x)=\sum_{m=1}^{M}c_{m}I(x\in R_{m}) \]
\[ \hat{c}_{m}=\mathrm{ave}(y_{i}\mid x_{i}\in R_{m}) \]
- splitting variable
- splitting point
\[ R_{1}(j,s)=\{x\mid x^{(j)}\leqslant s\}\quad\text{和}\quad R_{2}(j,s)=\{x\mid x^{(j)}>s\} \]
\[ \min_{j,s}\biggl[\min_{c_{1}}\sum_{x_{i}\in R_{i}(j,s)}(y_{i}-c_{1})^{2}+\min_{c_{2}}\sum_{x_{i}\in R_{2}(j,s)}(y_{i}-c_{2})^{2}\biggr] \]
\[ \hat{c}_{1}=\mathrm{ave}(y_{i}\mid x_{i}\in R_{1}(j,s))\quad\hat{\text{和}}\quad\hat{c}_{2}=\mathrm{ave}(y_{i}\mid x_{i}\in R_{2}(j,s)) \]
5.5.2 CART 剪枝 ¶
- 剪枝,形成一个子树序列
\[ C_{\alpha}(T)=C(T)+\alpha\left|T\right| \]
\[ g(t)=\frac{C(t)-C(T_{t})}{\mid T_{t}\mid-1} \]
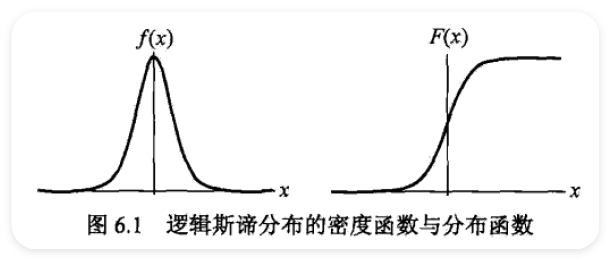
6 逻辑斯谛回归与最大熵模型 ¶
- logistic regression
- maximum entropy model
- 逻辑斯谛回归模型和最大熵模型都属于对数线性模型